Supporting Learning Difficulties in Mathematics / Dyscalculia
Many would ask why I would be equally as interested in supporting learning difficulties in Mathematics as I am in supporting learning difficulties in Literacy. Interestingly, Jane Emerson who wrote the Dyscalculia Solution and The Dyscalculia Assessment is a Speech Pathologist with a special interest in Mathematics Learning Difficulties from the UK.
As a part of my upcoming presentation for the Dyslexia SPELD Conference which goes live on Easter Tuesday, I’ve been reading the recently published book by Dr Valerie Muter, titled Understanding and Supporting Children with Literacy Difficulties: An Evidence-Based Guide for Practitioners. Dr Muter has spent 15 years working as a consultant neuropsychologist at Great Ormond St Hospital for Children in the UK and has also partnered in much research with Professor Margaret Snowing. If you work with Tier 3 students in a clinic or school based intervention setting this is a must read book.

But I digress, I have recently shared my near point reference for supporting students who struggle with recall of Multiplication and Division Facts. It is also extremely useful for supporting understanding of Division with remainder, multiples and factors. The image below comes from Dr Muter’s book, p. 97 [see above]
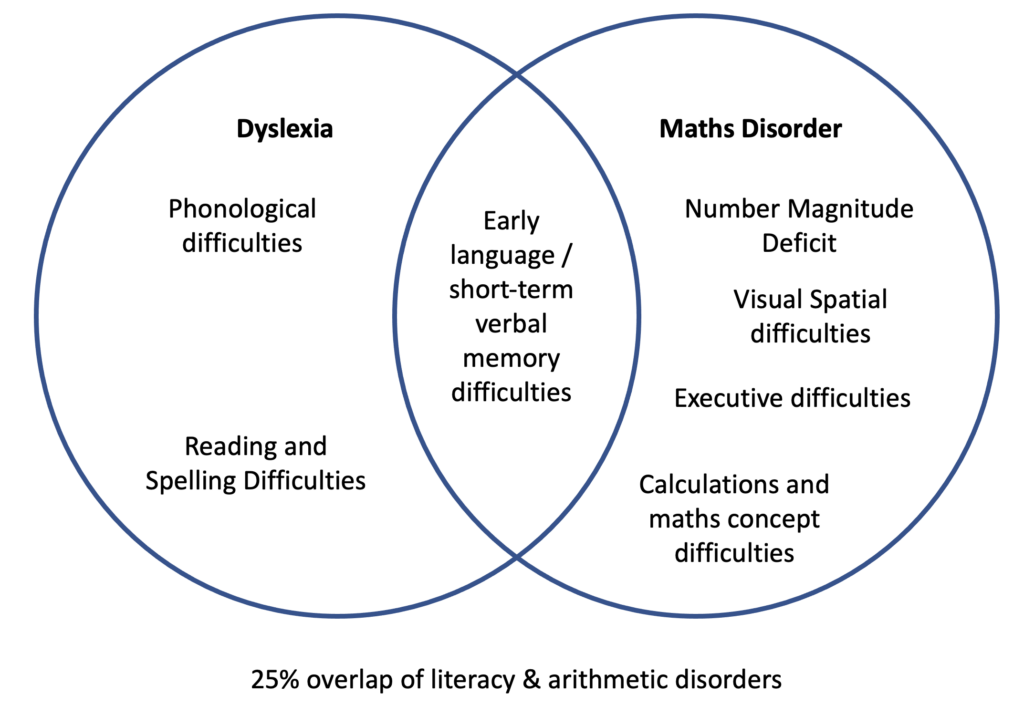
For our students with both Dyslexia and Maths Disorder [also known as Dyscalculia] recall of Mathematical Fact knowledge, especially Multiplication and Division facts is going to be a challenge. Too often we allow these difficulties to prevent a student from progressing to learning more advanced mathematical computation skills. It is increasingly common for schools to be using online mathematics programs to ‘teach’ mathematics in lieu of a specialist mathematics teacher and unfortunately a ‘mastery of maths facts’ requirement means that for some students where their Math Disorder is a lifelong disability they aren’t given the opportunity to progress in their development of mathematical computational skills because they don’t have the required basic facts retrieval fluency so the ‘online program’ creates an artificial ‘ceiling effect’.
Another concept to consider which I was reminded of when I completed Multisensory Math 1 with Marilyn Zecher, is that recall of numbers by rote is actually a word retrieval or language based naming task rather than a mathematical computational task. Therefore, if a student has difficulties with language, a ‘skill and drill’ approach isn’t going to assist them to progress.
Back in 2002, when I completed my Masters in Special Education, I completed my final project on the impact of Language Impairment on the development of Mathematical Skills. Back then research indicated that best practice was the Concrete – Representational / Semi-Concrete – Abstract instruction sequence. My near point reference that you can access below supports students to move beyond the concrete stage of Multiplication and Division Facts to provide them with a Representational or Semi Concrete tool to support their ability to progress to learning more advanced mathematical computational skills. To update it, I have also provided it formatted for use on See Saw and I will shortly add a Google Slides Version.
Once consideration for assessment: Do you structure your assessment tasks so that you can identify whether the student has difficulty with the process of fact knowledge [ie. retrieval] or mathematical computational skills. To do this with my struggling upper primary students, I would regularly set assessment tasks that included two parts – eg. 1. Map the 6 times tables on the hundreds chart provided 2. Use this information to complete multiplication and division tasks or answer questions about factors, multiples and complete tasks involving division with remainder. What I observed was that students who would typically ‘melt’ and task avoid would engage and across the school year they would shift to working without the near point reference tool as their self confidence and accuracy of recall improved. Furthermore, students could see their progress and knew that they weren’t ‘hopeless at all mathematics’ but rather they struggled to recall certain table facts.
You can download the free resource here and over time I will add to the collection